|
Электро Динамика Элементов из Металла |
ЭДЭМ |
||
программа для расчета электромагнитных полей и исследования электродинамических свойств структур из проводящих элементов |
|||
| [главная страница] [возможности] [математический аппарат] [как работать с программой] [демонстрационная версия] [статьи] |
О возможностях новой версии программного комплекса EDEM. 1. Аннотация. Существенно расширены возможности программного комплекса EDEM3D [1] для исследования электродинамических характеристик проводящих объектов - металлических рефлекторов, экранов, замкнутых и незамкнутых оболочек и объемных тел. Реализованы алгоритмы решения плоских двумерных задач, а также задач для поверхностей вращения; добавлены новые возможности для анализа трехмерных задач. Анализируемые объекты могут быть не только идеально проводящими, но и иметь поглощающие и импедансные покрытия и содержать сосредоточенные емкости и индуктивности. Возможно решение задач для бесконечных решеток из таких объектов.
2. Новые возможности для решения трехмерных задач. Персональные компьютеры уже достигли такого уровня, что в тех случаях, когда использование интегральных уравнений для анализа задачи вообще имеет смысл, редко приходится сталкиваться с недостатком возможностей компьютера при решении двумерных задач и задач для поверхностей вращения. Длина контура исследуемых поверхностей здесь может составлять десятки и сотни длин волн. В то же время при решении трехмерных задач недостаток памяти и слишком большое время решения являются главным ограничивающим фактором. В рассматриваемой версии реализованы специальные алгоритмы, позволяющие во многих случаях увеличить размеры анализируемой системы поверхностей при фиксированных возможностях компьютера. В первую очередь это относится к использованию симметрии. Если решение заведомо симметрично относительно какой-либо плоскости, можно задать лишь независимую часть исходной системы и указать вид симметрии, после чего EDEM сам достроит модель и использует для решения метод, дающий четырехкратную экономию оперативной памяти и существенное уменьшение времени решения. Точно так же можно использовать антисимметрию, когда половина решения является зеркальным отражением другой его половины. Можно также использовать комбинацию этих видов (см. пример расчета) и получить весьма существенный выигрыш. Весьма эффективным для тех задач, где это возможно, является использование симметрии поворота на угол p/n вокруг некоторой оси, где n –целое число. Это дает экономию памяти в n 2 раз. На практике нередко встречаются случаи, когда само решение не обязательно обладает симметрией, но исходная структура может быть образована повторением некоторой своей части конечное число раз. Например, это может быть решетка из конечного числа элементов. EDEM может эффективно использовать эту специфику, сводя задачу к системе линейных уравнений с теплицевыми матрицами, что также дает экономию памяти и уменьшение времени решения. Другую группу составляют возможности, позволяющие, используя физические соображения, разбить большую задачу на несколько более мелких и применить метод последовательных приближений. При этом результаты расчета поля одной задачи можно использовать в качестве первичного поля для другой задачи. В данной версии реализованы алгоритмы решения задач для бесконечных периодических решеток. Элемент решетки при этом может представлять собой объект произвольной трехмерной формы с импедансным покрытием, сосредоточенными нагрузками и т.п. Реализованы также некоторые приближенные подходы к решению задачи, в частности метод физической оптики для определения наведенных токов.
3. Работа с комплексом. Рассматриваемая версия комплекса EDEM предназначена для работы под управлением операционных систем Windows 9X и NT. Задача решается в общем случае в пять этапов. Результаты каждого этапа могут отображаться на экране, при этом можно возвращаться назад для исправления ошибок, внесения корректив в исходные данные и т.п. На первом этапе создается исходное задание (либо корректируется созданное ранее). Для этого используется простой язык, приближенный к используемому в учебной и научно-технической литературе. В задании задаются проводящие объекты, источники возбуждения - плоские волны, точечные источники, линейные вибраторы и т.п., а также определяются требуемые результаты решения. Например, задать рассеиватель в виде треугольной пластины, определив предварительно точки вершин, можно следующим образом: p1:(1,0,1); p2:(0,0,1); p3:(0,1,1); trn1:(p1,p2,p3);
При определении рассеивателей с трехмерной геометрией можно использовать элементы в виде треугольников, параллелограммов, вытянутых полос, четырехугольников произвольного вида, дисков и их секторов, плоских колец, круговых цилиндров, цилиндрических и конических спиралей. При определении контуров рассеивателей для цилиндрических задач, а также для поверхностей вращения можно использовать отрезки прямых, окружностей, эллипсов, гипербол, парабол, а также сплайн-функции, построенные на основе заданных точек. Пор умолчанию рассеиватели считаются идеально проводящими. Можно задавать имепедансные
поверхности и поверхности с поглощающими пленками, явно указав в задании значение
величины
Имеется ряд возможностей, упрощающих составление задания. Так, те или иные объекты можно сдвигать и поворачивать, а также репродуцировать – повторять требуемое число раз.
На втором этапе блок обработки задания строит исходную модель и отображает ее на экране. При этом он контролирует возможные ошибки и неточности, и в случае их обнаружения генерирует соответствующие сообщения, прерывая процесс и предоставляя возможность вернуться к первому этапу внести исправления. На третьем этапе строится расчетная сетка. В простейшем случае для этого не требуется предоставлять дополнительную информацию в задании – EDEM делает это в автоматическом режиме. Построенная сетка отображается на экране. При необходимости в задании можно явно задать информацию, определяющую требуемый вид сетки. На четвертом этапе решаются интегральные уравнения и находится распределение наведенных токов. Этот этап является самым длительным при решении задачи. Если для прохождения этапов 1-3 требуются доли секунды, на этом этапе при большом количестве элементов сетки могут потребоваться минуты и часы расчетного времени. На последнем, пятом этапе в соответствии с заданием рассчитываются необходимые характеристики полей: амплитудные
и фазовые распределения различных их компонент, диаграммы направленности и т.п.
Большое внимание уделено визуализации полученных результатов. Найденные распределения плотностей токов могут изображаться в виде линейных диаграмм, в трехмерных задачах – также в виде карты амплитуд и с помощью получившей в настоящее время распространение цветовой шкалы. В этом случае поверхность рассеивателей отображается цветом от красного до темно-синего в зависимости от амплитуды наведенных в той или иной области токов. Отображение распределения компонент полей реализовано в виде линейных диаграмм, в виде двумерных рельефов или с помощью цветовой шкалы, а также с помощью комбинации этих способов.
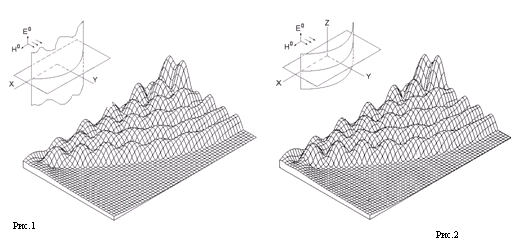
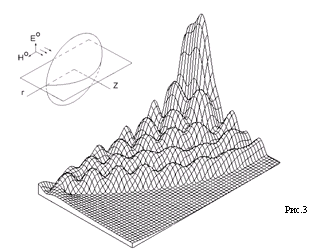
Рис.1 приведен для параболического цилиндра с бесконечной образующей (плоская двумерная задача). На рис.2 показаны результаты решения трехмерной задачи для параболического цилиндра конечных размеров, приведен рельеф распределения Z-составляющей электрического поля в плоскости XOZ. Рис.3 соответствует параболоиду вращения, рельеф приведен для Н-плоскости. Контуры параболической образующей во всех трех случаях одинаковы, раскрыв параболы имеет размер 10 длин волн, отношение фокусного расстояния к величине раскрыва 0.25. Высота параболического цилиндра в случае трехмерной задачи составляет 6 длин волн. Время определения плотности токов на компьютере Pentium с тактовой частотой 200 МГц в случае двумерной задачи составило 16 сек, в случае параболоида вращения 1 мин. 36 сек. При решении трехмерной задачи одновременно использовалась симметрия решения относительно плоскости XOZ и антисимметрия относительно плоскости XOY. Это дало 16-кратную экономию оперативной памяти, уравнение решалось для 1620 элементов сетки , время решения составило 3 час.42 мин.
|
| Контакты: info@edem3d.ru
|
|
|
| Создание и поддержка сайта: Дефи |